A venturi meter is a flow measuring equipment or gadget that is used to measure the discharge of liquid through a pipe. It is based on Bernoulli’s principle.
Table of Contents
Construction:
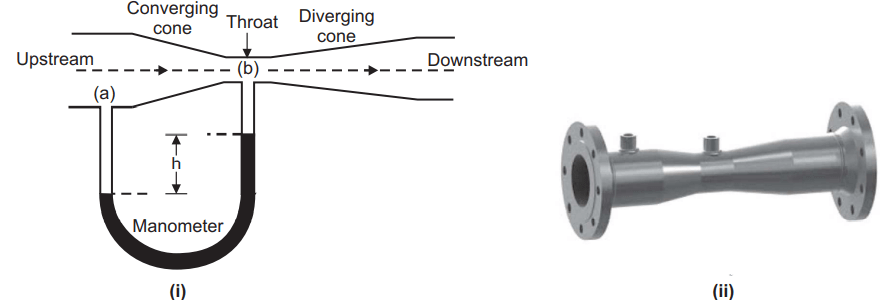
A venturi meter is essentially a small pipe with two conical portions and a short segment of the uniform cross-section in between, as shown in Fig. 1.14. The neck is the smallest part of the body with the smallest area. The two conical parts have the same base diameter, but one is shorter and has a greater cone angle, while the other is longer and has a smaller cone angle.
Working of Venturi Meter:
The upstream and downstream variation in the conical component assures a rapid converging passage and a gradual diverging passage in the flow direction. This is simply to prevent energy waste due to throat separation. During a flow through the converging phase, the speed increases in the flow direction, following the principle of continuity, but the pressure falls, following Bernoulli’s theorem. At the throat, the velocity hits its peak and the pressure drops to its lowest point. As a result, in the course of flow through the divergent region, there is a decrease in velocity and an increase in pressure. A venturi meter is put in an inclined pipeline in a vertical plane to measure the flow rate through the pipe, as shown in Fig. 1.15. Consider a fluid flow that is steady, ideal, and one-dimensional (along the axis of the venturi metre). The velocity and pressure at any segment will be uniform in this condition.
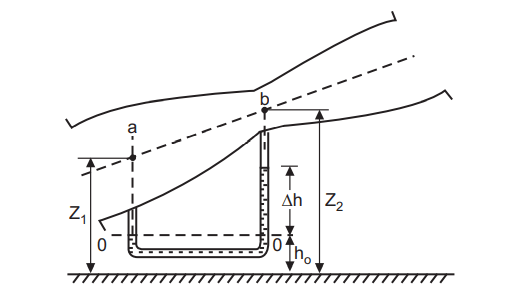
Let the velocity and pressure at the inlet (a) be V1 and P1, respectively, while those at the throat (b) are V1 and P2. Now, applying Bernoulli’s equation between (a) and (b), we get
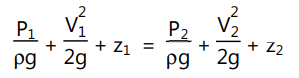
… (1.35)
V1 A1 = V2 A2 ….(1.36)
where A1 and A2 are the cross-sectional areas of the venturi meter at its throat and inlet respectively.
With the help of equation (1.35), equation (1.36) can be written as
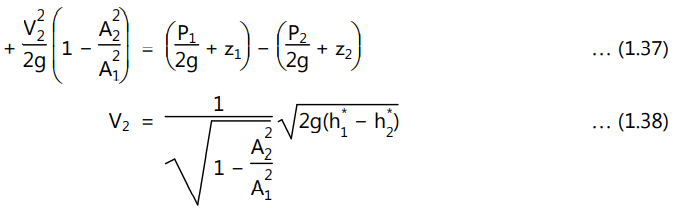
where, h1 and h2 are the piezometric pressure heads at (a) and (b), respectively, and are defined as

Hence, the volume flow rate through the pipe is given by
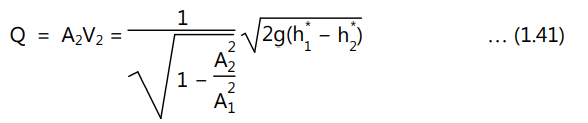
If the pressure difference between (a) and (b) is measured by a manometer as shown in Figure. 1.14, we can write
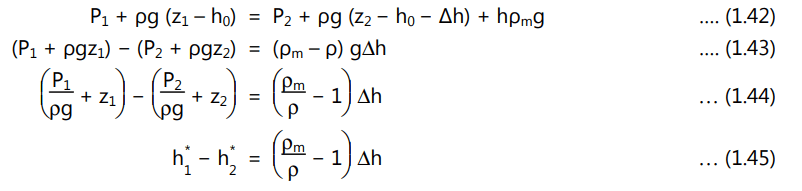
where ρm is the density of the manometric liquid. The equation (1.45) shows that a manometer always registers a direct reading of the difference in piezometric pressures. Now, the substitution of h1 – h2 from equation (1.45) in equation (1.44) gives,
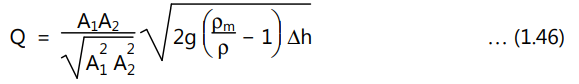
If the pipe along with the venturi meter is horizontal, then z1 = z2; and hence h1 – h2 becomes h1 – h2, where h1 and h2 are the static pressure heads.

Thus, manometric equation (1.45) becomes,

Whether the pipeline and venturi meter connection is horizontal or not, the final expression of flow rate given by equation (1.46) in terms of manometer deflection h remains the same. Because of frictional losses and the change in momentum, the measured values of h, the difference in piezometric pressures between (a) and (b), for a real fluid will always be greater than for an ideal fluid. As a result, the real flow rate is always overestimated by equation (1.46). To account for this, the coefficient of discharge (Cd) is included in the equation (1.46) as a multiplication factor (Cd).

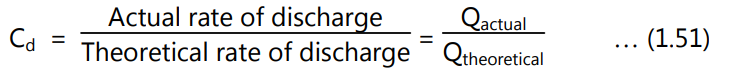
Where Eq. (1.46) predicts the theoretical discharge rate given the measured value of h, and the actual discharge rate is the discharge rate measured in practice. The Cd value for a venturi meter is normally between 0.95 and 0.98.
Applications:
- Venturimeter can be used for the measurement of flow of water, liquids, gases, dirtyliquids etc.
- They are commonly used in water supply industry.
Advantages/Merits of Venturi Meter:
- It has low head loss of about 10% of differential pressure head.
- It can measure higher flow rates in pipes having few meters of diameters due to high coefficient of discharge owing to lower loss.
- It is suitable for use in any position, for example, horizontal, vertical or inclined.
- Higher sensitivities can be achieved due to smaller size throat which leads to higher pressure differential.
Disadvantages/demerits of Venturi Meter:
- It has space limitations due to larger size.
- Due to large size, the cost of venturimeter is higher.
- Very small diameter of throat results into cavitations of fluid in the throat.
- It is more susceptible to errors due to burrs or deposits round the downstream (throat) tapping.