Bernoulli’s theorem and its applications

Bernoulli’s Theorem

Bernoulli’s theorem is the principle of energy conservation for ideal fluids in steady or streamlined inflow. This theorem describes the relationship among pressure, haste, and elevation in a moving fluid similar to liquid or gas. According to this theorem, the compressibility and density ( internal disunion) are negligible and the inflow is steady, or laminar. First deduced (1738) by the Swiss mathematician Daniel Bernoulli, the theorem states that the total mechanical energy of the flowing fluid comprises the energy associated with fluid pressure, the gravitational implicit energy of elevation, and the kinetic energy of fluid remains constant. In simple terms, Bernoulli’s theorem can be described as within a vertical inflow of fluid, points of advanced fluid speed will have lower pressure than points of slower fluid speed’.

Incompressible fluids have to speed up when they reach a narrow constricted section in order to maintain a constant volume inflow rate. This is why a narrow snoot on a sock causes water to speed up. If the water is speeding up at a condensation means it’s gaining kinetic energy. To give kinetic energy is to do work. So if a portion of the fluid is speeding up, a commodity external to that portion of fluid must be doing work it. For illustration, consider that water flows along streamlines from left to right, Fig.1.8. As the outlined volume of water enters the constricted region it speeds up. The force from pressure P1 on water pushes to the right and does positive work. The force from pressure P2 on the fluid pushes to the left and does negative work since it pushes on the contrary direction as the stir of the fluid.

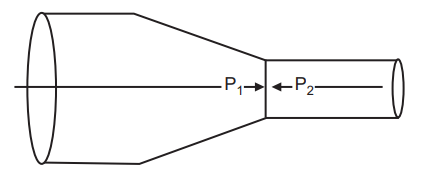
The pressure on the wider/slower side P1 has to be larger than the pressure on the narrow/faster side P2. This inverse relationship between the pressure and speed at a point in a fluid is called Bernoulli’s principle.

Bernoulli’s Equation/Bernoulli’s Theorem :

Bernoulli’s equation is a general and fine form of Bernoulli’s principle that takes into account changes in gravitational implicit energy. Bernoulli’s equation relates the pressure, speed, and height of any two points (1 and 2) in a steady streamline flowing fluid of viscosity‘ρ’.

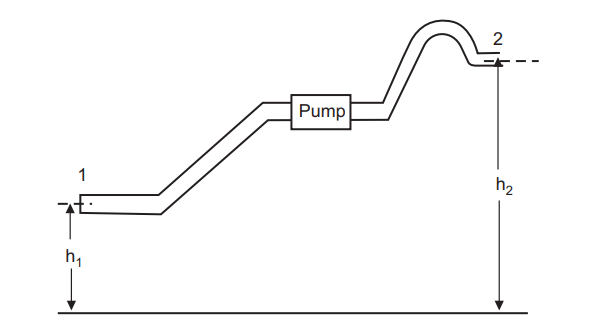
Bernoulli’s theorem investigates the distribution of pressure in a moving incompressible fluid.

For a case, consider that throughout the system, the periphery of the pipe and the temperature is constant. Fig.1.9 represents a channel conveying a fluid from point 1 to point 2. The pump provides energy to beget the inflow in an upward direction. Assume that one pound of fluid enters the channel at point 1. The pressure at this point is P₁lb/ft ². If the average haste of fluid is V₁ lb/ sec and the specific volume of fluid is V₁ft ³/ lb. Point 1 is at height h1 above the vertical bottom aeroplane. The implicit energy of a pound of fluid at point 1 is equal to h1ft. lb. Since the fluid is in stir with haste V1, a pound of fluid will have a kinetic energy equal to V² ₁/2gc ft.lb. This expression is grounded on the average haste (V) of the fluid in the system. In reality, the average haste differs from the mean haste. The kinetic energy per pound of fluid flowing in the channel is given by

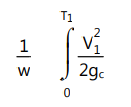
where, w is the weight of fluid in the system, r1 is the radius of the channel and VL is the local velocity at distance r from the axis of the channel. As we know, the distribution of velocity varies widely within the channel at different localities, the true integral is obtained only when the actual velocity distribution is known. For each case, a different velocity distribution curve is obtained. Thus, the kinetic energy in the real sense is written as V ²/ αgc, where α is a correction factor for variations in velocities at different locations in the channel. It was found that for viscous flow α = 1 and for turbulent flow α = 2.

Since one pound of fluid enters the channel, it enters against pressure P₁ lb/ft², and therefore work is equal to P ₁ V ₁ ft.lb done on one pound of fluid and is added to the implicit energy. The sum of all three powers represents the energy of one pound of fluid entering the section of the channel. According to the principle of conservation of mass whenever the system reaches a steady-state, and when one pound fluid enters at point 1, another pound of fluid is displaced at point 2. The energy content of fluid leaving at point 2 can be expressed as

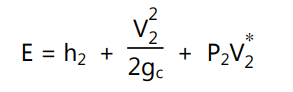
where, V2 is velocity, P2 is pressure and V2 specific volume of fluid at point 2.

If there is no gain or loss of energy in the system between points 1 and 2 it follows the principle of conservation energy. But it has been postulated that the energy is added by the pump. This energy is ‘W’ ft.lb/lb of fluid. Some of the energy is converted into heat by friction and dissipated into the environment through radiation as the system is at a constant temperature. The loss of energy due to friction is ‘F’ ft.lb/lb of fluid. The total energies of the system under consideration that balances between points 1 and 2 will be

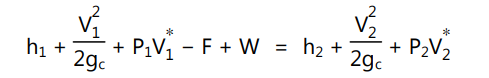
If the density of fluid ‘ρ’ is expressed as lb/ft³ , then

Then the equation (1.22) becomes,

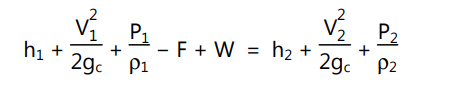
This expression is based on the consideration of one pound of fluid entering the system and all energy terms in the above equation (1.23) are per pound mass of fluid.

Applications of Bernoulli’s Equation

• Bernoulli’s equation allows us to estimate the flow rate of fluid through a pipe.
• It allows us to measure the change in velocity and pressure experienced by a fluid running from a pipe of some cross-sectional area into a pipe of a different cross sectional area. A fluid will have increased velocity and decreased pressure as it flows from a bigger pipe to a smaller pipe. This relationship is especially important in preventing a malfunction in water pipes through maintaining the stable fluid pressure. If the pressure is too high, the pipe explodes causing damage and other problems.
• It can be used to calculate the lift force on an airfoil, if the behaviour of the fluid flow in the vicinity of the foil is known.
• The Pitot tube and static port on an aircraft are used to determine the air speed of the aircraft. Bernoulli’s principle is used to calibrate the air speed indicator so that it displays the indicated air speed appropriate to the dynamic pressure
• A De Laval nozzle utilizes Bernoulli’s principle to create a force by turning pressure energy generated by the combustion of propellants into velocity.
• The flow speed of a fluid can be measured using a device such as a Venturi meter or an orifice plate, which can be placed into a pipeline to reduce the diameter of the flow. For an incompressible fluid, the reduction in diameter may cause an increase in the fluid flow speed. Bernoulli’s principle shows that there must be a decrease in the pressure in the reduced diameter region.
• The maximum possible drain rate for a tank with a hole or tap at the base can be calculated directly from Bernoulli’s equation, and is found to be proportional to the square root of the height of the fluid in the tank. Viscosity lowers this drain rate. This is reflected in the discharge coefficient, which is a function of the Reynolds number and the shape of the orifice.
• The Bernoulli grip relies on this principle to create a non-contact adhesive force between a surface and the gripper.