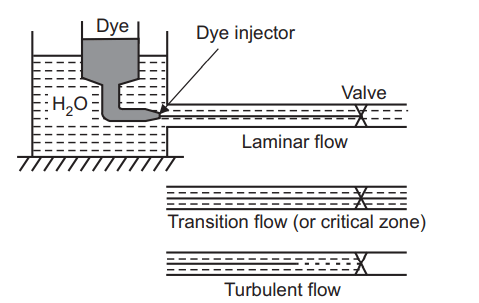
Reynolds number
The non-dimensional parameter called Reynolds number was discovered by an Irish engineer and physicist, Osborne Reynolds, in 1883. He identified the fundamental dimensionless parameter that characterizes the behavior of flowing fluids, known as the Reynolds number. It was the ratio that shows the effect of viscosity in a given medium that governs the transition between laminar and turbulent flow. Before this invention, it was believed that turbulent flow occurs in pipes of large cross-sectional dimensions and flows at high velocities, whereas laminar flow occurs in slow flows in pipes of relatively small cross-sectional dimensions. The role of viscosity and density in affecting the type of motion is not well-characterized.
According to Reynolds, in laminar flux, the pressure drop is direct in the average haste of the fluid, whereas in turbulent flux it’s roughly commensurate to V1.72, where V is the average haste. The factual dependence of the pressure drop on the haste of turbulent flux in circular pipes is more complicated. The roughness of the interior pipe wall in contact with the fluid affects the pressure drop. He proposed that the change in the nature of the flux occurs when a certain combination of the parameters in the flux crosses a threshold. This combination was named after his name as the Reynolds number. For flux in a circular pipe of fringe’D’ at an average haste ofhaste’V’, the Reynolds number’Re’is defined as follows,
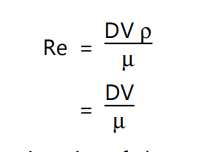
Then, ‘µ’is the dynamic density of the fluid, and‘ρ’is the viscosity of the fluid. The rate‘Vρ/ µ’is called as kinematic density. For indirect tubes, the transition from laminar to turbulent inflow occurs over a range of Reynolds figures from roughly to, anyhow of the nature of the fluid or the confines of the pipe or the average haste but is dependent of combination of the parameters known as the Reynolds number that falls in the range. Therefore, when the Reynolds number is below, the inflow is laminar, and when it’s above, the inflow is turbulent. In between these two limits, the inflow is nominated to be transition inflow.
Reynolds number can be ascribed a physical significance if multiplied both the numerator and the denominator by the average velocity V as follows.
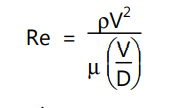
The above equation denominator represents a characteristic shear stress in the flow as it is the product of the viscosity of the fluid and a characteristic velocity gradient obtained by dividing the average velocity by the diameter of the tube. On the other hand the numerator describes an inertial stress. This is the reason for calling the product ‘2ρV’ a characteristic inertial stress. Thus, the Reynolds number as the ratio of two characteristic stresses in the flow.
Re =Inertial stress/Viscous stress
Stress is force per unit area. Therefore, the physical significance of the Reynolds number is expressed as follows.
Re =Inertia force/Viscous force
The nature of the inflow in a tube, whether laminar or turbulent, depends on the relative significance of the indolence force in comparison with the thick force. At fairly low values of the Reynolds numbers, the thick force is fairly more important, and disturbances in the inflow are compensated by density. Therefore, it’s delicate for disturbances to grow and sustain themselves. On the other hand, at fairly large values of the Reynolds number, the damping of disturbances by density is less effective, and indolence is more important, so that disturbances can immortalize themselves. Therefore, Reynolds number serves as a measure for determining the type of inflow ( i.e., laminar or turbulent). The use of the periphery in the description of the Reynolds number is an arbitrary choice. The length of the tube in defining the Reynolds number is considered because the typical haste variation in this inflow is across the sampling of the tube and not along its length. Therefore, if we had used the length’L’, the reality’ (V/ L)’would not be representative of the shear stress in this inflow.
Reynolds number for the steady motion of a sphere through a fluid:
When dimensional analysis is performed on the drag experienced by a sphere of diameter ‘dp’ moving at a velocity ‘V’ through a fluid with viscosity ‘µ’ and density ‘ρ’, a Reynolds number in this situation is defined as:
Re =dpVp/µ
The drag measure, which is a dimensionless drag, depends on this Reynolds number. The inflow past a sphere is more involved than that in a tube. At high Reynolds number, a boundary subcaste, in which thick goods are important, forms on the sphere, and outside of this boundary subcaste, thick goods are fairly insignificant, and the inflow is dominated by indolence. The low haste for simple and ordered inflow indicates that Re should be low. Hence, laminar inflow takes place when ρ, V and L are small and µ is large. The inflow turns out to be turbulent from laminar if the haste is increased, keeping all other parameters constant. Since Reynolds’ number is directly commensurable to haste, the inflow should be a direct function of haste. Still, the pressure drop which these types of inflow produce while flowing in a pipe doesn’t follow the linearity in case of turbulent inflow. Therefore the relation between pressure drop and haste is expressed as
∆P α V for laminar flow
∆P α V2 for turbulent flow
Make sure check our amazing article: What is manometer and its types