Sommerfeld atomic model: When spectrometers were used to study spectra, each line was discovered to be made up of many closely packed lines. On the basis of Bohr’s hypothesis, the occurrence of these numerous spectral lines could not be explained. Sommerfeld made the following changes to Bohr’s theory. Although Bohr regarded electron orbits to be circular, Sommerfeld proposed that they might possibly be elliptic. A major and minor axis exists in an ellipse. A circle is an ellipse with equal major and minor axes, which is a particular case of an ellipse. An electron’s angular momentum in an elliptic orbit is likewise intended to be quantized. As a result, only a specific set of values is permitted. Furthermore, it is believed that angular momentum can have a component of h/2 units, where h is Planck’s constant. Alternatively,
angular momentum=kh/2 π
where k is called the azimuthal quantum number, whereas the quantum number used in Bohr’s theory is called the principal quantum number. The two quantum numbers n and k are related by the expression :
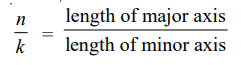
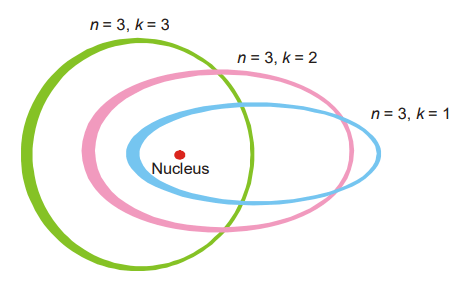
The values of k for a given value of n are k = n – 1, n – 2, n – 3, and so on. A series of elliptic orbits with different eccentricities results in different values of k. When n = k, the orbit will be circular. In other words, k will have n possible values (n to 1) for a given value of n. However, calculations based on wave mechanics have shown that this is incorrect and the Sommerfeld’s modification of the Bohr atom fell through.