The nuclear model of Rutherford essentially claimed that an atom had a nucleus and that the negative electrons were present outside the nucleus. It made no mention of how or where the electrons were organized. It also couldn’t explain why, despite electrostatic pull, electrons didn’t fall into the nucleus. Niels Bohr presented a new model of the atom in 1913, which described some of these phenomena as well as the hydrogen emission spectrum. The following postulates underpin Bohr’s hypothesis, which is based on Planck’s quantum theory.
Table of Contents
Postulates of Bohr’s Theory
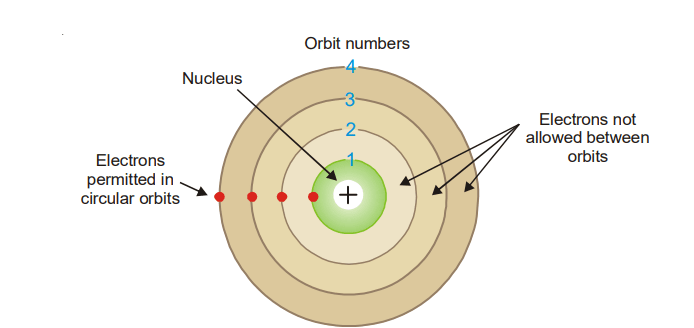
(1) Electrons travel around the nucleus in specific permitted circular orbits and in no others.
Each orbit contains electrons with a given energy and a fixed distance from the nucleus. As the distance from the nucleus rises, the orbits are given the letter n and are numbered 1, 2, 3, etc. (or K, L, M, etc.).
(2) While in these specific orbits, an electron does not radiate (or lose) energy.
As a result, an electron’s energy remains constant in each of these orbits, i.e. it does neither lose nor gain energy. As a result, the electron’s particular orbits in an atom are referred to as stationary energy levels or simply energy levels.
(3) An electron can move from one energy level to another by quantum or photon jumps only.
The electron is considered to be in the ground state when it is in the lowest-energy orbit (which is also the one nearest to the nucleus). An electron receives one quantum or photon of energy and leaps to a higher energy level when it is given energy. The electron is therefore considered to be stimulated since it possesses potential energy.
The quantum or photon of energy absorbed or emitted is the difference between the lower and higher energy levels of the atom
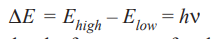
……1
where h is Planck’s constant and ν the frequency of a photon emitted or absorbed energy.
(4) The angular momentum (mvr) of an electron orbiting around the nucleus is an integral multiple of Planck’s constant divided by 2π.
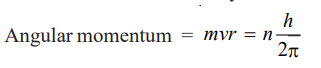
……. 2
where m = mass of electron, v = velocity of the electron, r = radius of the orbit ; n = 1, 2, 3, etc., and h = Planck’s constant.
By putting the values 1, 2, 3, etc., for n, we can have respectively the angular momentum
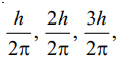
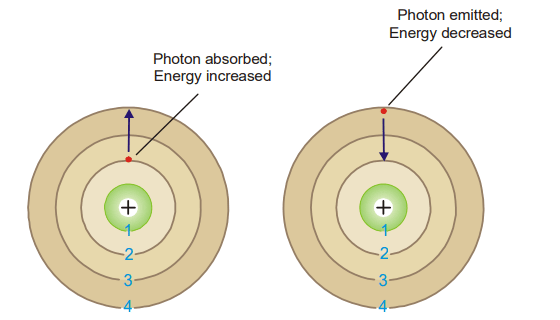
orbit and a photon is emitted while it returns to the original lower energy level. (Bohr’s Theory)
Bohr was able to determine the radius of each orbit of the hydrogen atom, the energy associated with each orbit, and the wavelength of the radiation emitted in transitions between orbits using the aforementioned postulates and certain classical physics equations. This technique calculates wavelengths.
The Bohr model was discovered to be in great agreement with those in the actual hydrogen spectrum, which was a huge success.
Calculation of radius of orbits
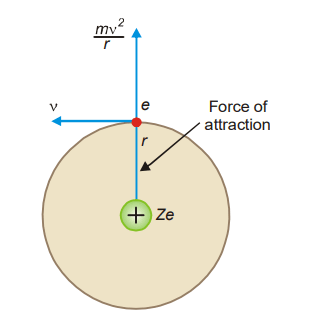
Consider an e-charged electron circling around a Ze-charged nucleus, where Z is the atomic number and e is the charge on a proton. Let m be the electron’s mass, r the orbit’s radius, and v be the tangential velocity of the rotating electron.
The electrostatic force of attraction between the nucleus and the electron (Coulomb’s law), = Ze.e/r2
The centrifugal force acting on the electron= mv2 /r
Bohr assumed that these two opposing forces must be balancing each other exactly to keep the electron in orbit. Thus,
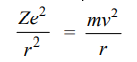
For hydrogen Z = 1, therefore,
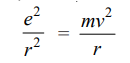
Multiplying both sides by r
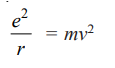
According to one of the postulates of Bohr’s theory, the angular momentum of the revolving electron is given by the expression
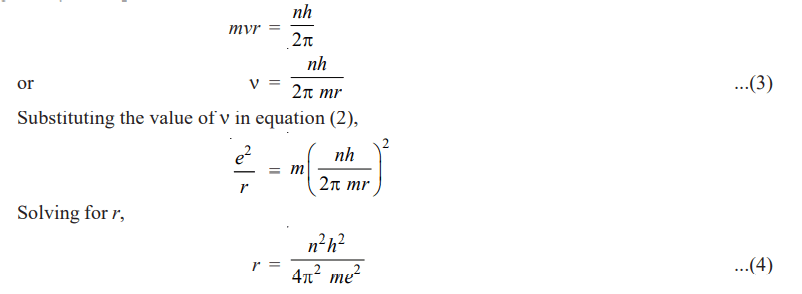
Since the value of h, m and e had been determined experimentally, substituting these values in (4), we have
r = n2 × 0.529 × 10-18 cm ……(5)
r = 0.529 × 10-8 cm = αo ……(6)
This last quantity, α0 called the first Bohr radius was taken by Bohr to be the radius of the hydrogen atom in the ground state. This value is reasonably consistent with other information on the size of atoms. When n = 2, 3, 4, etc., the value of the second and third orbits of hydrogen comprising the electron in the excited state can be calculated.
Energy of electron in each orbit
For the hydrogen atom, the energy of the revolving electron, E is the sum of its kinetic energy (½ mv2) and potential energy (-e2 /r).
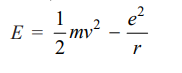
……(7)
From equation (1)
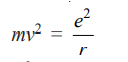
Substituting the value of mv2 in (7)
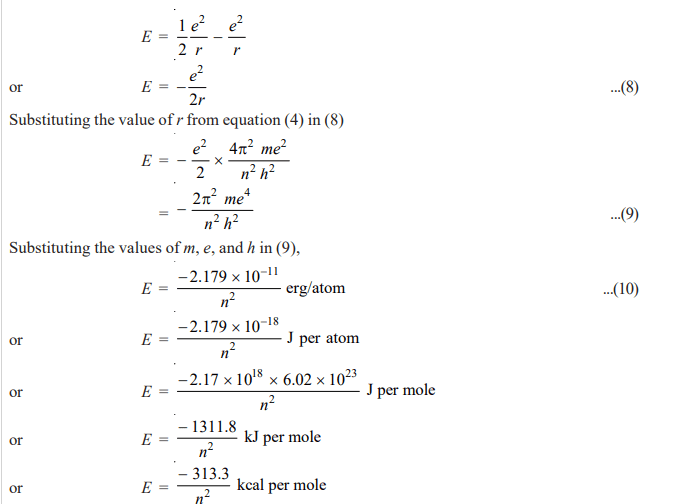
By using a proper integer for n (quantum or orbit number), we can get the energy for each orbit.
Significance of Negative Value of Energy
At infinity, the energy of an electron is arbitrarily considered to be zero. This is referred to as a zero-energy condition. When an electron moves and comes into contact with a nucleus, it works and expends energy in the process. As a result, the electron’s energy drops and falls below zero, resulting in a negative value.