Drugs are in a dynamic state within the body as they move between tissues and fluids, bind with plasma or cellular components, or are metabolized. The biological nature of drug distribution and disposition is complex, and drug events often happen simultaneously. Such factors must be considered when designing drug therapy regimens. The inherent and infinite complexity of these events requires the use of mathematical models and statistics to estimate drug dosing and to predict the time course of drug efficacy for a given dose.
A model is a hypothesis using mathematical terms to describe quantitative relationships concisely.
The predictive capability of a model lies in the proper selection and development of mathematical function(s) that parameterizes the essential factors governing the kinetic process. The key parameters in a process are commonly estimated by fitting the model to the experimental data, known as variables. A pharmacokinetic parameter is a constant for the drug that is estimated from the experimental data.
For example, estimated pharmacokinetic parameters such as k depend on the method of tissue sampling, the timing of the sample, drug analysis, and the predictive model selected.
A pharmacokinetic function relates an independent variable to a dependent variable, often through the use of parameters. For example, a pharmacokinetic model may predict the drug concentration in the liver 1 hour after an oral administration of a 20-mg dose. The independent variable is the time and the dependent variable is the drug concentration in the liver. Based on a set of time-versus-drug concentration data, a model equation is derived to predict the liver drug concentration with respect to time. In this case, the drug concentration depends on the time after the administration of the dose, where the time–
concentration relationship is defined by a pharmacokinetic parameter, k, the elimination rate constant.
Such mathematical models can be devised to simulate the rate processes of drug absorption, distribution, and elimination to describe and predict drug concentrations in the body as a function of time. Pharmacokinetic models are used to:
- Predict plasma, tissue, and urine drug levels with any dosage regimen
- Calculate the optimum dosage regimen for each patient individually
- Estimate the possible accumulation of drugs and/or metabolites
- Correlate drug concentrations with pharmacologic or toxicologic activity
- Evaluate differences in the rate or extent of availability between formulations (bioequivalence)
- Describe how changes in physiology or disease affect the absorption, distribution, or elimination of the drug
- Explain drug interactions
Simplifying assumptions are made in pharmacokinetic models to describe a complex biologic system concerning the movement of drugs within the body. For example, most pharmacokinetic models assume that the plasma drug concentration reflects drug concentrations globally within the body.
A model may be empirically, physiologically, or compartmentally based. The model that simply interpolates the data and allows an empirical formula to estimate drug level over time is justified when limited information is available. Empirical models are practical but not very useful in explaining the mechanism of the actual process by which the drug is absorbed, distributed, and eliminated in the body.
Physiologically based models also have limitations. Using the example above, and apart from the necessity to sample tissue and monitor blood flow to the liver in vivo, the investigator needs to understand the following questions. What is the clinical implication of the liver drug concentration value? Should the drug concentration in the blood within the tissue be determined and subtracted from the drug in the liver tissue? What type of cell is representative of the liver if a selective biopsy liver tissue sample can be collected without contamination from its surroundings? Indeed, depending on the spatial location of the liver tissue from the hepatic blood vessels, tissue drug concentrations can differ depending on the distance to the blood vessel or even on the type of cell in the liver. Moreover, changes in the liver blood perfusion will alter the tissue drug concentration. If heterogeneous liver tissue is homogenized and assayed, the homogenized tissue represents only a hypothetical concentration that is an average of all the cells and blood in the liver at the time of collection. Since tissue homogenization is not practical for human subjects, the drug concentration in the liver may be estimated by knowing the liver extraction ratio for the drug based on knowledge of the physiologic and biochemical composition of the body organs. A great number of models have been developed to estimate regional and global information about drug disposition in the body. Individual pharmacokinetic processes are discussed in separate chapters under the topics of drug absorption, drug distribution, drug elimination, and pharmacokinetic drug interactions involving one or all of the above processes. Theoretically, an unlimited number of models may be constructed to describe the kinetic processes of drug absorption, distribution, and elimination in the body, depending on the degree of detailed information considered. Practical considerations have limited the growth of new pharmacokinetic models.
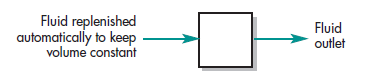
with drug.
A very simple and useful tool in pharmacokinetics is compartmentally based models. For example, assume a drug is given by intravenous injection and that the drug dissolves (distributes) rapidly in the body fluids. One pharmacokinetic model that can describe this situation is a tank containing a volume of fluid that is rapidly equilibrated with the drug. The concentration of the drug in the tank after a given dose is governed by two parameters: (1) the fluid volume of the tank that will dilute the drug, and (2) the elimination rate of the drug per unit of time. Though this model is perhaps an overly simplistic view of drug disposition in the human body, a drug’s pharmacokinetic properties can frequently be described using a fluid-filled tank model called the one-compartment open model (see below). In both the tank and the one compartment body model, a fraction of the drug would be continually eliminated as a function of time (Fig. 1-5). In pharmacokinetics, these parameters are assumed to be constant for a given drug. If drug concentrations in the tank are determined at various time intervals following administration of a known dose, then the volume of fluid in the tank or compartment (VD, volume of distribution) and the rate of drug elimination can be estimated.In practice, pharmacokinetic parameters such as k and VD are determined experimentally from a set of drug concentrations collected over various times and known as data. The number of parameters needed to describe the model depends on the complexity of the process and on the route of drug administration. In general, as the number of parameters required to model the data increases, accurate estimation of these parameters becomes increasingly more difficult. With complex pharmacokinetic models, computer programs are used to facilitate parameter estimation. However, for the parameters to be valid, the number of data points should always exceed the number of parameters in the model.
Because a model is based on a hypothesis and simplifying assumptions, a certain degree of caution is necessary when relying totally on the pharmacokinetic model to predict drug action. For some drugs, plasma drug concentrations are not useful in predicting drug activity. For other drugs, an individual’s genetic differences, disease state, and the compensatory response of the body may modify the response to the drug. If a simple model does not fit all the experimental observations accurately, a new, more elaborate model may be proposed and subsequently tested. Since limited data are generally available in most clinical situations, pharmacokinetic data should be interpreted along with clinical observations rather than replacing sound judgment by the clinician. The development of pharmacometrics statistical models may help to improve the prediction of drug levels among patients in the population (Sheiner and Beal, 1982; Mallet et al, 1988). However, it will be some time before these methods become generally accepted.
Table of Contents
Compartment Models
If the tissue drug concentrations and binding are known, physiologic pharmacokinetic models, which are based on actual tissues and their respective blood flow, describe the data realistically. Physiologic pharmacokinetic models are frequently used in describing drug distribution in animals because tissue samples are easily available for assay. On the other hand, tissue samples are often not available for human subjects, so most physiological models assume an average set of blood flow for individual subjects.
In contrast, because of the vast complexity of the body, drug kinetics in the body are frequently simplified to be represented by one or more tanks, or compartments, that communicate reversibly with each other. A compartment is not a real physiologic or anatomic region but is considered a tissue or group of tissues that have similar blood flow and drug affinity. Within each compartment, the drug is considered to be uniformly distributed. Mixing of the drug within a compartment is rapid and homogeneous and is considered to be “well stirred,” so that the drug concentration represents an average concentration, and each drug molecule has an equal probability of leaving the compartment. Rate constants are used to represent the overall rate processes of drug entry into and exit from the compartment. The model is an open system because drugs can be eliminated from the system. Compartment models are based on linear assumptions using linear differential equations.
Mammillary Model
A compartmental model provides a simple way of grouping all the tissues into one or more compartments where drugs move to and from the central or plasma compartment. The mammillary model is the most common compartment model used in pharmacokinetics. The mammillary model is a strongly connected system because one can estimate the amount of drug in any compartment of the system after the drug is introduced into a given compartment. In the one-compartment
model, the drug is both added to and eliminated from a central compartment. The central compartment is assigned to represent plasma and highly perfused tissues that rapidly equilibrate with drugs. When an intravenous dose of the drug is given, the drug enters directly into the central compartment. Elimination of drugs occurs from the central compartment because the organs involved in drug elimination, primarily the kidney and liver, are well-perfused tissues.
In a two-compartment model, the drug can move between the central or plasma compartment too and from the tissue compartment. Although the tissue compartment does not represent a specific tissue, the mass balance accounts for the drug present in all the tissues. In this model, the total amount of drugs in the body is simply the sum of the drug present in the central compartment plus the drug present in the tissue compartment. Knowing the parameters of either the one-compartment or the two-compartment model, one can estimate the amount of drug left in the body and the amount of drug eliminated from the body at any time. The compartmental models are particularly useful when little information is known about the tissues.
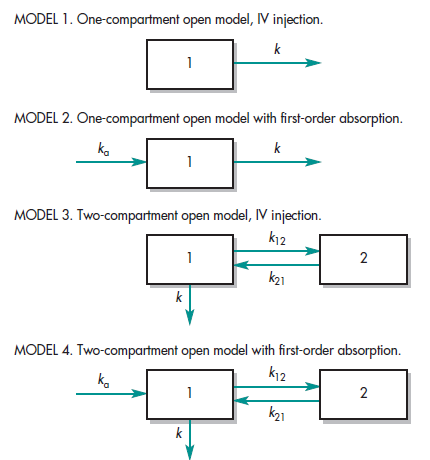
Several types of compartment models are described in Fig. 1-6. The pharmacokinetic rate constants are represented by the letter k. Compartment 1 represents the plasma or central compartment, and compartment 2 represents the tissue compartment. The drawing of models has three functions. Model (1) enables the pharmacokinetics to write differential equations to describe drug concentration changes in each compartment, (2) gives a visual representation of the rate processes, and (3) shows how many pharmacokinetic constants are necessary to describe the process adequately.
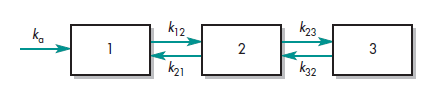
Catenary Model
In pharmacokinetics, the mammillary model must be distinguished from another type of compartmental model called the catenary model. The catenary model consists of compartments joined to one like the compartments of a train (Fig. 1-7). In contrast, the mammillary model consists of one or more compartments around a central compartment like satellites. Because the catenary model does not apply to the way most functional organs in the body are directly connected to the plasma, it is not used as often as the mammillary model.
Physiologic Pharmacokinetic Model (Flow Model)
Physiologic pharmacokinetic models, also known as blood flow or perfusion models, are pharmacokinetic models based on known anatomic and physiologic data. The models describe the data kinetically, with the consideration that blood flow is responsible for distributing drugs to various parts of the body. The uptake of drugs into organs is determined by the binding of drugs in these tissues. In contrast to an estimated tissue volume of distribution, the actual tissue volume is used. Because there are many tissue organs in the body, each tissue volume must be obtained and its drug concentration described. The model would potentially predict realistic tissue drug concentrations, which the two-compartment model fails to do. Unfortunately, much of the information required for adequately describing a physiologic pharmacokinetic model is experimentally difficult to obtain. In spite of this limitation, the physiologic pharmacokinetic model does provide much better insight into how physiologic factors may change drug distribution from one animal species to another. Other major differences are described below.
First, no data fitting is required in the perfusion model. Drug concentrations in the various tissues are predicted by organ tissue size, blood flow, and experimentally determined drug tissue–blood ratios (ie, partition of drug between tissue and blood). Second, blood flow, tissue size, and the drug tissue–blood ratios may vary due to certain pathophysiologic conditions. Thus, the effect of these variations on drug distribution must be taken into account in physiologic pharmacokinetic models. Third, and most important of all, physiologically based pharmacokinetic models can be applied to several species, and, for some drugs, human data may be extrapolated. Extrapolation from animal data is not possible with the compartment models, because the volume of distribution in such models is a mathematical concept that does not relate simply to blood volume and blood flow. To date, numerous drugs (including digoxin, lidocaine, methotrexate, and thiopental) have been described with perfusion models. Tissue levels of some of these drugs cannot be predicted successfully with compartment models, although they generally describe blood levels well. An example of a perfusion model is shown in Fig. 1-8.
The number of tissue compartments in a perfusion model varies with the drug. Typically, the tissues or organs that have no drug penetration are excluded from consideration. Thus, such organs as the brain, the bones, and other parts of the central nervous system are often excluded, as most drugs have little penetration into these organs. To describe each organ separately with a differential equation would make the model very complex and mathematically difficult. A simpler but equally good approach is to group all the tissues with similar blood perfusion properties into a single compartment.
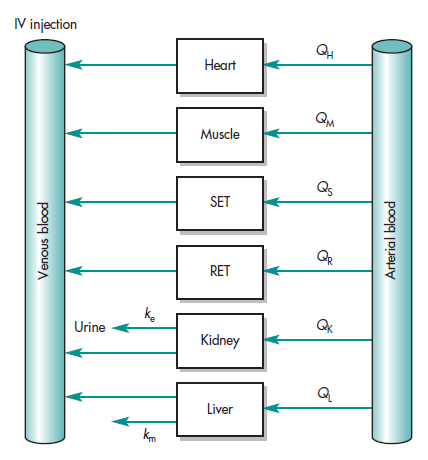
A physiologic-based pharmacokinetic model (PBPK) using known blood flow was used to describe the distribution of lidocaine in blood and various organs (Benowitz et el 1974) and applied in anesthesiology in man (Tucker et el 1971). In PBKB models, organs such as lung, liver, brain, and muscle were individually described by differential equations as shown in Fig. 1-8, sometimes tissues were grouped as RET (rapidly equilibrating tissue) and SET (slowly equilibrating tissue) for simplicity to account for the mass balance of the drug. A general scheme showing blood flow for typical organs is shown in Fig. 1-8.
The data showing the blood concentration of lidocaine after an IV dose declining biexponentially (Fig. 1-9) was well predicted by the model. A later PBPK model was applied to model cyclosporine (Fig. 1-10). Drug levels in various organs were well predicted and scaled to humans based on this physiologic model (Kawai R et al, 1998). The tissue cyclosporine levels in the lung, muscle, and adipose, and other organs are shown in Fig. 1-10. For lidocaine, tissue such as adipose (fat) tissue accumulates drugs slowly because of low blood supply. In contrast, vascular tissues, like the lung, equilibrate rapidly with the blood and start to decline as soon as drug level in the blood starts to fall resulting in curvature of plasma profile. The physiologic pharmacokinetic model provides a realistic means of modeling tissue drug levels. However, drug levels in tissues are not available. A criticism of physiologic pharmacokinetic models, in general, has been that there are fewer data points than parameters that one tries to fit. Consequently, the projected data are not well constrained.
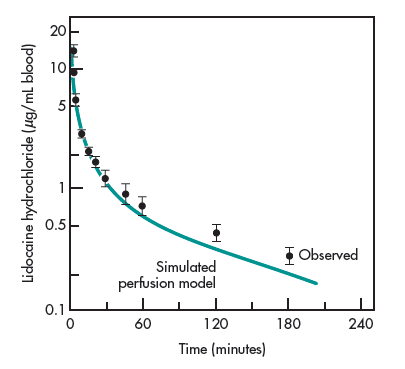
arterial lidocaine blood concentrations
The real significance of the physiologically based model is the potential application of this model in the prediction of human pharmacokinetics from animal data (Sawada et al, 1985). The mass of various body organs or tissues, the extent of protein binding, drug metabolism capacity, and blood flow in humans and other species are often known or can be determined. Thus, physiologic and anatomic parameters can be used to predict the effects of drugs on humans from the effects on animals in cases where human experimentation is difficult or restricted. drug metabolism capacity, and blood flow in humans and other species are often known or can be determined. Thus, physiologic and anatomic parameters can be used to predict the effects of drugs on humans from the effects on animals in cases where human experimentation is difficult or restricted.
More sophisticated models are introduced as the understanding of human and animal physiology improves. For example, special compartment models that take into account transporter-mediated drug disposition are introduced for specific drugs. This approach is termed Physiologic Pharmacokinetic Model Incorporating Hepatic Transporter-Mediated Clearance. The differences between the physiologic pharmacokinetic model, the classical compartmental model, and the non-compartmental approach are discussed. It is important to note that mass transfer and balances of drugs in and out of the body or body organs are fundamentally a kinetic process. Thus, the model may be named as physiologically based when all drugs distributed to body organs are identified. For data analysis, parameters are obtained quantitatively with different assumptions. One approach is to classify models simply as empirically-based models and mechanistic models. Although compartment models are critically referred to as a “black box” approach and not physiological. The versatility of compartment models and their easy application are based on simple mass transfer algorithms or a system of differential equations. This approach has allowed many body processes such as binding, transport, and metabolic clearance to be monitored. In Appendix B, softwares used for various type of model analysis are discussed, for example, noncompartmental analysis is often used for pharmacokinetic and bioavailability data analysis for regulatory purpose.