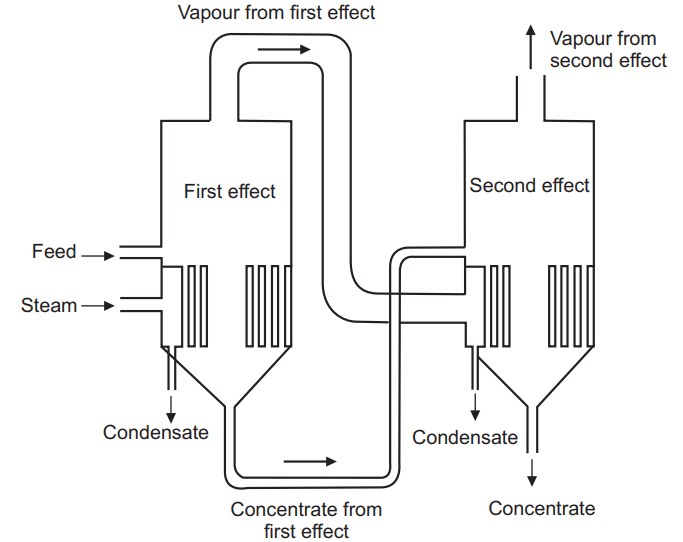
The performance of multiple effect evaporators is measured in terms of its capacity and economy. The capacity of the evaporator is defined as the number of kilograms of water vaporized per hour. Its economy is the number of kilograms of water vaporized from all the effects per kilogram of steam used. For a single effect evaporator, the steam economy is approximately about 0.8 (<1). The capacity is about n-times that of a single effect evaporator, and the economy is about 0.8 n for n-effect evaporators. However, pumps, interconnecting pipes, and valves required for the transfer of liquid from one effect to another effect increases both the equipment and the operating costs.
The economy of multiple effect evaporators is greater than single effect because vapors generated in the first effect are used as a heating medium for the second effect and so on. Thus, efficiency increases as steam consumption decreases and evaporative capacity increases.
At first sight, it may seem that the multiple-effect evaporator has all the advantages, the heat is used over and over again and it appears to be getting the evaporation in the second and subsequent effects for nothing in terms of energy costs. However, the fact is that there is a price to be paid for the heat economy. For example;
In the first effect, q1 = U1 A1 ∆T1 —–(5.7)
In the second effect, q2 = U2 A2 ∆T2 —–(5.8)
We shall now consider a single-effect evaporator, working under the same pressure as the first effect
Qs = Us As ∆Ts ——-(5.9)
Where subscript ‘s’ indicates the single-effect evaporator. Since the overall conditions are the same,
∆Ts = ∆T1 + ∆T2 ——(5.10)
As the overall temperature drop is between the steam-condensing temperature in the first effect and the evaporating temperature in the second effect. Each successive steam chest in the multiple-effect evaporator condenses at the same temperature at which the previous effect is evaporating. Now, consider the case in which U1 = U2 = Us, and A1 = A2.
As for the single-effect evaporator that will evaporate the same quantity as in the two effects is obtained as follows. From the given conditions and from equation (U2 /U1 = T1 /T2)—-(5.6),
∆T1 = ∆T2 —–(5.11)
and ∆Ts = ∆T1 + ∆T2 —–(5.12)
= 2∆T1
∆T1 = 0.5∆Ts —–(5.13)
Now, q1 + q2 = U1 A1 ∆T1 + U2 A2 ∆T2
= U1 (A1 + A2) ∆Ts / 2 ——(5.14)
But, q1 + q2 = qs and qs = U As ∆Ts
So that, (A1 + A2)/ 2 = 2A1 / 2 = As —–(5.15)
That is A1 = A2 = As
The analysis shows that if the same total quantity is to be evaporated, then the heat transfer surface of each of the two effects must be the same as that for a single effect evaporator. In multiple effect evaporators, steam economy has to be paid for by increased capital costs of the evaporators. Since the heat transfer areas are generally equal in the various effects and since in a sense what you are buying in an evaporator is suitable heat transfer surface, the n effects will cost approximately n times as much as a single effect.
| Number of effects | Steam consumption (kg steam/kg water evaporated) | Total running cost (relative to a single-effect evaporator) |
| One | 1.1 | 1 |
| Two | 0.57 | 0.52 |
| Three | 0.40 | 0.37 |
Comparative costs of the auxiliary equipment do not altogether follow the same pattern. Condenser requirements are less for multiple effect evaporators. The condensation duty is distributed between the steam chests of the effects, except for the first one, and so condenser and cooling water requirements will be less. The optimum design of evaporation plant is based on a balance between operating costs which are lower for multiple effects because of their reduced steam consumption, and capital charges which will be lower for fewer evaporators. The comparative operating costs are illustrated by the figures in Table above. If the capital costs are known they would reduce the advantages of the multiple effects, but certainly not remove them.