Photoelectric effect
When a sufficiently high-frequency beam of light is permitted to impact a metal surface in a vacuum, electrons are expelled from the metal surface. The expelled electrons are known as Photoelectrons, and the process is known as the Photoelectric effect. The photoelectric effect, for example, happens when ultraviolet light shines on Cs (or Li, Na, K, Rb) as shown in the setup below.
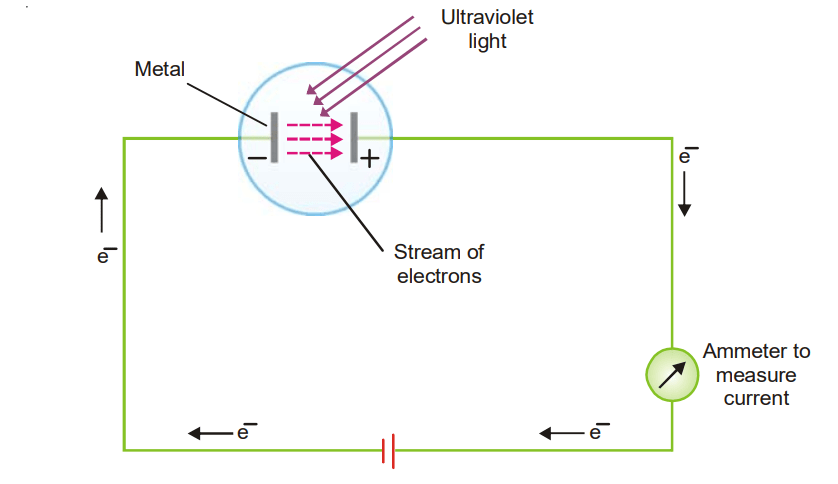
With the help of this photoelectric apparatus the following observations can be made :
- The energy of the photoelectrons does not rise as the intensity of incoming light increases. It just raises their emission rate.
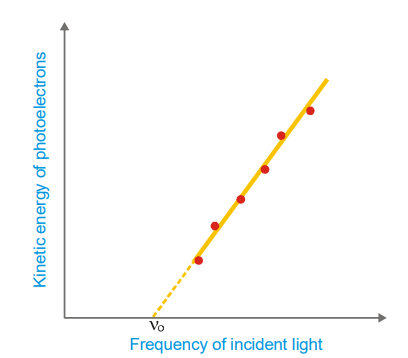
- The photoelectrons’ kinetic energy rises in lockstep with the frequency of the incoming light. No electrons are expelled if the frequency is reduced below a specific critical threshold (Threshold frequency, v0).
Classical Physics predicts that the kinetic energy of the photoelectrons should depend on the intensity of light and not on the frequency. Thus it fails to explain the above observations.
Einstein’s explanation of the photoelectric effect
Albert Einstein, who won the Nobel Prize for his work on photons in 1905, used the Quantum Theory of Light to explain the Photoelectric Effect.
- A photon of incident light transmits its energy (hν) to an electron in the metal surface which escapes with kinetic energy 1/2mv2. The greater intensity of incident light merely implies a greater number of photons each of which releases one electron. This increases the rate of emission of electrons, while the kinetic energy of individual photons remains unaffected.
- The incoming photon must first overcome the attractive attraction imposed by the metal’s positive ion in order to liberate an electron from the metal surface. The frequency of incoming light determines the energy of a photon (hv). The threshold frequency, 0 is the frequency that gives just enough energy to liberate the electron off the metal surface. There will be no electrons released if the frequency is less than 0.
For higher frequencies, ν > ν0, a part of the energy goes to loosen the electron and remaining for imparting kinetic energy to the photoelectron. Thus, hv=hv0 +1/2mv2 …….(1).
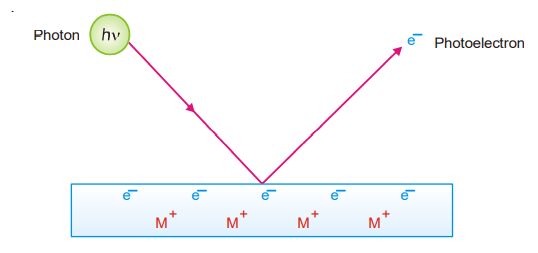
Where hν is the energy of the incoming photon, hv0 is the minimum energy for an electron to escape from the metal, and 1/2mv2 is the kinetic energy of the photoelectron. hν0 is constant for a particularly solid and is designated as W, the work function. Rearranging equation. (1)
1/2mv2 =hν – W …….(2).
This is the equation for a straight line that was experimentally obtained in the second figure. Its slope is equal to h, the Planck’s constant. The value of h thus found came out to be the same as was given by Planck himself.
Make sure check our amazing article on: The atomic spectrum of hydrogen