ph is the negative log of the hydrogen ion concentration

pH is the negative log of the hydrogen ion concentration

The term pH was introduced in 1909 by Sörensen, who defined it as the negative log of the hydrogen ion concentration: pH= -log[H⁺]

This definition, while not rigorous, suffices for many biochemical
purposes. To calculate the pH of a solution:

• Calculate the hydrogen ion concentration [H⁺]
• Calculate the base 10 logarithms of [H+].
• pH is the negative of the value found in step 2.

For example, for pure water at 25°C, pH= -log[H⁺]= -log10^-7 = -(-7)= 7.0.

This value is also known as the power (English), puissant (French), or potennz (German) of the exponent, hence the use
of the term “p.”
Low pH values correspond to high concentrations of [H⁺] and high pH values correspond to low concentrations of [H⁺]. Acids are proton donors and bases are proton acceptors. Strong acids (eg, HCl, H2SO4) completely dissociate into anions and protons even in strongly acidic solutions (low pH). Weak acids dissociate only partially in acidic solutions. Similarly, strong bases (eg, KOH, NaOH), but not weak bases like Ca(OH)2, are completely dissociated even at high pH. Many biochemicals are weak acids. Exceptions include phosphorylated intermediates, whose phosphoryl group contains two dissociable protons, the first of which is strongly acidic. The following examples illustrate how to calculate the pH of acidic and basic solutions.
Example 1: What is the pH of a solution whose hydrogen ion concentration is 3.2 × 10^-4 mol/L?

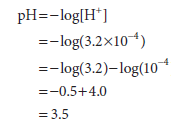
Example 2: What is the pH of a solution whose hydroxide ion concentration is 4.0 ×10^-4 mol/L? We first define a quantity pOH that is equal to -log[OH^–] and that may be derived from the definition of Kw:

Functional Groups That Are Weak Acids Have Great Physiologic Significance

Many biochemicals possess functional groups that are weak acids or bases. Carboxyl groups, amino groups, and phosphate esters, whose second dissociation falls within the physiologic range, are present in proteins and nucleic acids, most coenzymes, and most intermediary metabolites. Knowledge of the dissociation of weak acids and bases thus is basic to understanding the influence of intracellular pH on the structure and biologic activity. Charge-based separations such as electrophoresis and ion-exchange chromatography are also best understood in terms of the dissociation behavior of functional groups.

We term the protonated species (HA or R—NH₃⁺) the acid and the unprotonated species (A^– or R—NH2) its conjugate base. Similarly, we may refer to a base (A- or R—NH2) and its conjugate acid (HA or R—NH3⁺).

We express the relative strengths of weak acids and bases in terms of their dissociation constants. Shown below are the expressions for the dissociation constant (Ka) for two representative weak acids, R—COOH and R—NH₃⁺ )

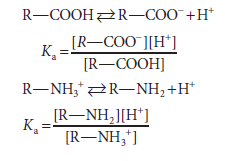
Since the numeric values of Ka for weak acids are negative exponential numbers, we express Ka as pKa, where

pKa = -logKa

Note that pKa is related to Ka as pH is to [H+]. The stronger the acid, the lower is its pKa value. Representative weak acids (left), their conjugate bases (center), and pKa values (right) include the following:

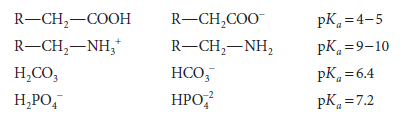
pKa is used to express the relative strengths of both acids and bases. For any weak acid, its conjugate is a strong base. Similarly, the conjugate of a strong base is a weak acid. The relative strengths of bases are expressed in terms of the pKa of their conjugate acids. For polyprotic compounds containing more than one dissociable proton, a numerical subscript is assigned to each dissociation, numbered starting from unity in decreasing order of relative acidity. For dissociation of the type

R´NH₃⁺—-R´NH2 +H⁺

the pKa is the pH at which the concentration of the acid R—NH3⁺ equals that of the base R—NH2. From the above equations that relate Ka to [H⁺] and to the concentrations of undissociated acid and its conjugate base, when

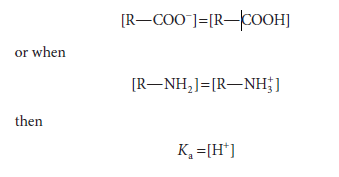
Thus, when the associated (protonated) and dissociated (conjugate base) species are present at equal concentrations, the prevailing hydrogen ion concentration [H⁺] is numerically equal to the dissociation constant, Ka. If the logarithms of both sides of the above equation are taken and both sides are multiplied by -1, the expressions would be as follows:

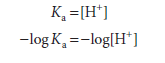
Since -log Ka is defined as pKa, and -log [H⁺] defines pH, the equation may be rewritten as

pKa = pH

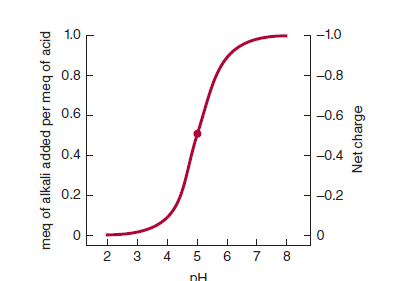
that is, the pKa of an acid group is the pH at which the protonated and unprotonated species are present at equal concentrations. The pKa for an acid may be determined by adding 0.5 equivalent of alkali per equivalent of acid. The resulting pH will equal the pKa of the acid.

The Henderson-Hasselbalch Equation Describes the Behavior of Weak Acids & Buffers

The Henderson-Hasselbalch equation is derived below. A weak acid, HA, ionizes as follows:

Inversion of the last term removes the minus sign and gives the Henderson-Hasselbalch equation

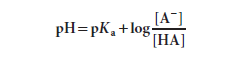
The Henderson-Hasselbalch equation has great predictive value in protonic equilibria. For example,

If the equation is evaluated at ratios of [A−]/[HA] ranging from 103 to 10−3 and the calculated pH values are plotted, the resulting graph describes the titration curve for a weak acid

Solutions of Weak Acids & Their Salts Buffer Changes in pH

Solutions of weak acids or bases and their conjugates exhibit buffering, the ability to resist a change in pH following the addition of strong acid or base. Many metabolic reactions are accompanied by the release or uptake of protons. Oxidative metabolism produces CO2, the anhydride of carbonic acid, which if not buffered would produce severe acidosis. Biologic maintenance of a constant pH involves buffering by phosphate, bicarbonate, and proteins, which accept or release protons to

resist a change in pH. For laboratory experiments using tissue extracts or enzymes, constant pH is maintained by the addition of buffers such as MES ([2-N-morpholino]-ethane sulfonic acid, pKa 6.1), inorganic orthophosphate (pKa2 7.2), HEPES (N-hydroxyethyl piperazine-N′-2-ethane sulfonic acid, pKa 6.8), or Tris (tris[hydroxymethyl]aminomethane, pKa 8.3). The value of pKa relative to the desired pH is the major determinant of
which buffer is selected.
Buffering can be observed by using a pH meter while titrating a weak acid or base. We can also calculate the pH shift that accompanies the addition of acid or base to a buffered solution. In the example below, the buffered solution (a weak acid, pKa = 5.0, and its conjugate base) is initially at one of four pH values. We will calculate the pH the shift that results when 0.1 meq of KOH is added to 1 meq of each solution:

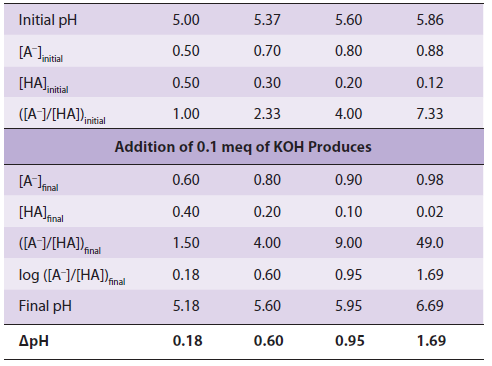
Notice that ΔpH, the change in pH per milliequivalent of OH− added, depends on the initial pH. The solution resists changes in pH most effectively at pH values close to the pKa. A solution of a weak acid and its conjugate base buffers most effectively in the pH range pKa ± 1.0 pH unit.

Also illustrates how the net charge on one molecule of the acid varies with pH. A fractional charge of −0.5 does not mean that an individual molecule bears a fractional charge but that the probability is 0.5 that a given molecule has a unit of the negative charge at any given moment in time. Consideration of the net charge on macromolecules as a function of pH provides the basis for separatory techniques such as ion-exchange chromatography and electrophoresis.

Acid Strength Dependson Molecular Structure

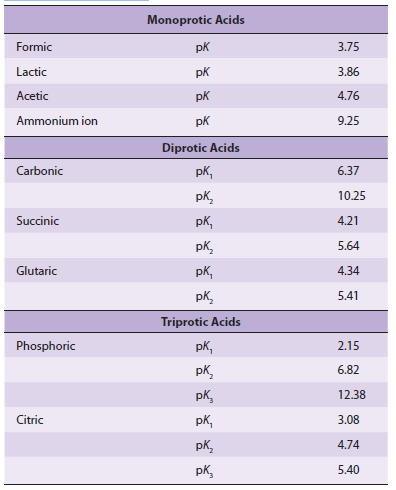
Many acids of biologic interest possess more than one dissociating group. The presence of a local negative charge hinders proton release from nearby acidic groups, raising their pKa. This is illustrated by the pKa values of the three dissociating groups of phosphoric acid and citric acid. The effect ofadjacent charge decreases with distance. The second pKa for

succinic acid, which has two methylene groups between its carboxyl groups, is 5.6, whereas the second pKa for glutaric acid, which has one additional methylene group, is 5.4.

pKa Values Depend on the Properties of the Medium

The pKa of a functional group is also profoundly influenced by the surrounding medium. The medium may either raise or lower the pKa relative to its value in water, depending on whether the undissociated acid or its conjugate base is the charged species. The effect of the dielectric constant on pKa may be observed by adding ethanol to water. The pKa of a carboxylic acid increases, whereas that of an amine decreases because ethanol decreases the ability of water to solvate a charged species. The pKa values of dissociating groups in the interiors of proteins thus are profoundly affected by their local environment, including the presence or absence of water.

Make sure also check our amazing article: Water Is An Excellent Nucleophile