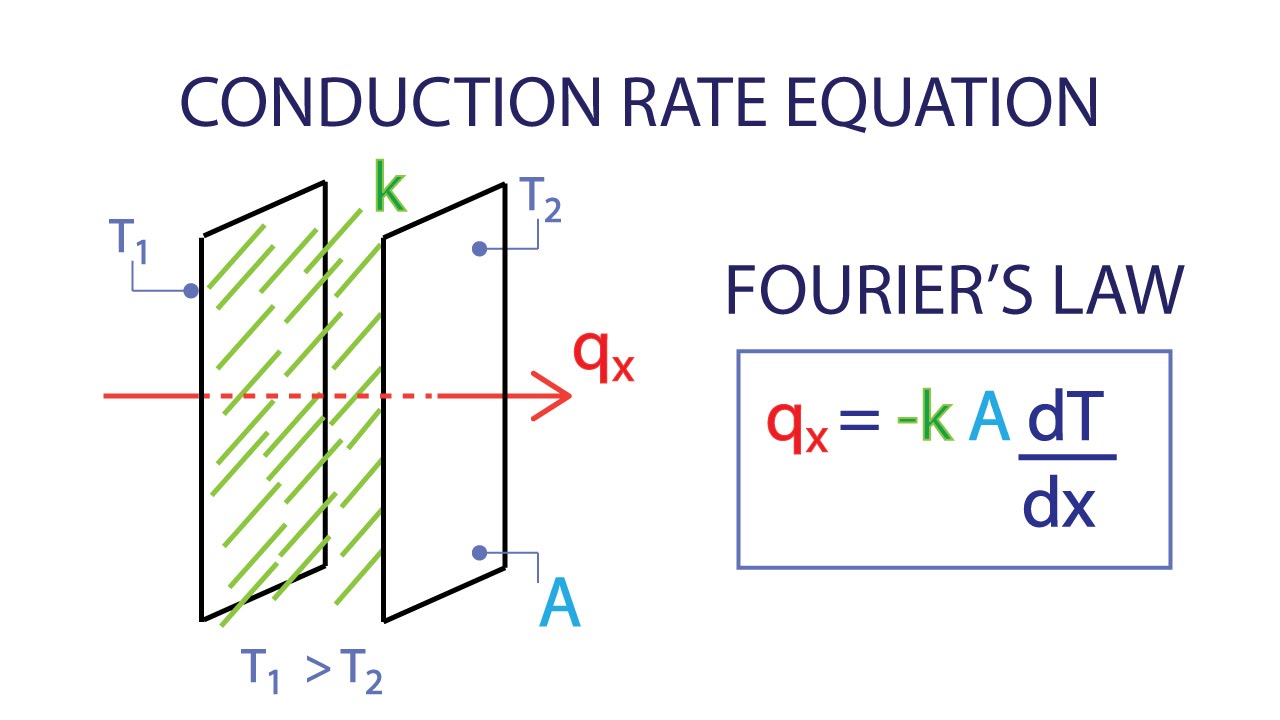
Fourier’s law is another name for the law of heat conduction. “The time rate of heat transmission through a material is proportional to the negative temperature gradient and to the area,” it says.
The Fourier’s equation of heat conduction is expressed as equation (4.1)
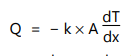
Where, Q is the heat flow rate by conduction (W), k is the thermal conductivity of body material (W/m.K), A is the cross-sectional area normal to direction of heat flow (m2) and dt/dx is the temperature gradient (K/m).
The negative sign in Fourier’s equation indicates that the heat flow is in the direction of negative gradient temperature and that serves to make heat flow positive. Thermalconductivity is one of the transport properties. Other properties includes viscosity associated with the transport of momentum and diffusion coefficient associated with the transport of mass. Thermal conductivity provides an indication of the rate at which heat energy is transferred through a medium by conduction process.
Steady state heat conduction, one-directional heat flow, isothermal bounding surfaces with constant and uniform temperatures on both faces, isotropic and homogeneous material and thermal conductivity constant, constant temperature gradient and linear temperature profile, and no internal heat generation are among the Fourier equation’s assumptions.
The Fourier equation is unusual in that it is valid for all matter, whether solid, liquid, or gaseous. The heat flow rate is normal to an isotherm and in the direction of decreasing temperature, as indicated by the vector expression. It is not derivable from the first principle and aids in the definition of the transport property ‘k’. Thermal resistance is proportional to thermal conductance and is related to heat conduction. Consider a plane wall with a thickness of L and a thermal conductivity of k on average. The temperature of the two surfaces of the wall is kept constant at T1 and T2. We have Tx for one-dimensional constant heat conduction through the wall. Then, for a wall with two surfaces, Fourier’s law of heat conduction is written as:

Where, Qwall is the heat flux through the plane (W), k is the materials conductivity (W/m.K), Lis the plane thickness (m) and A is the plane area (m2). Thermal resistance is a heat property and is a measurement of a temperature difference by which an object or material resists a heat flow. The thermal resistance (Rt) for conduction in a plane wall is defined as: Rt = L/kA
Where, k is the materials conductivity (W/m.K), L is the plane thickness (m) and A is the plane area (m2) .