Theory of filtration

Theories of filteration

Theory of filtration: Gas Filtration Theory, In Liquid Filtration Theory the Kozeny-Carman Equation, Poiseulle’s Law, and Darcy’s Equation.

The flow of any liquid through any porous medium offers resistance to its flow. The rate of filtration in such cases is expressed as;

Filtration\;rate=\frac{Driving\;force}{Resis\tan ce\;by\;filter\;medium}

The net driving force in filtration is the pressure above the medium minus the pressure below the medium. The resistance offered by the filter medium is not constant over the period of filtration as it goes on increasing with time due to particle deposition on the filter medium. Rate is expressed as the volume of filtrate per unit time as dv/dt.

Depending on dispersing (fluid) medium filtration theory is divided into two parts.

Gas Filtration Theory:

Gas filtration includes filtration of aerosol and lyosol. Membrane filters and nucleopore filters are used for gas filtration which works on three mechanisms.

(i) Diffusion deposition: In this mechanism, the path followed by individual small particles do not coincide with the streamlines of the fluid because of Brownian motion. With decreasing particle size the intensity of Brownian motion increases and thus as a consequence, the intensity of diffusion deposition also increases.

(ii) Direct interception: This mechanism involves finite-size particles. These particles are intercepted as they approach the collecting surface to a distance equal to its radius. A special case of this mechanism is the so-called ‘sieve effect’, or ‘sieve mechanism’.

(iii) Inertial deposition: The presence of a body in the flowing fluid results in a curvature of the streamlines in the neighborhood of the body. Because of their inertia, the individual particles do not follow the curved streamlines but are projected against the body and may deposit there. It is obvious that the intensity of this mechanism increases with increasing particle size and velocity of flow.

(iv) Gravitational deposition: Individual particles have a certain sedimentation velocity due to gravity. As a consequence, the particles deviate from the streamlines of the fluid, and owing to this deviation; the particles may touch a fiber.

(v) Electrostatic deposition: Both the particles and the fibers in the filter may carry electric charges. Deposition of particles on the fibers may take place because of the forces acting between charges or induced forces.

Liquid Filtration Theory:

The term filtration covers all processes in which a liquid containing suspended solid is freed of some or the entire solid when the suspension is drawn through a porous medium. Filtration is of two types namely; ‘Cake filtration’ where the proportion of solids in suspension is large and most of the particles are collected in the filter cake which can subsequently be detached from the medium and ‘Deep bed filtration’ where the proportion of solids is very small. For example, in water filtration, the particles are often considered as smaller than the pores of the filter medium and penetrate at a considerable depth for being captured.

Kozeny-Carman Equation:

In filtration because the particles forming the cake are small and the flow-through bed is slow, streamline conditions are almost invariably obtained, and therefore at any instant, it may be represented as Figure.

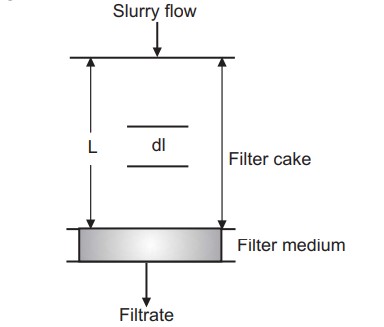
This is explained by Kozeny-Carman equation:

U=\;\frac1A\frac{dv}{dt}=\frac{\triangle P}{rµ\;(l\;+\;L)\;}

where, U = Flow rate

A = Filter area
v = Total volume of filtrate delivered
t = Filtration time
∆P = Pressure drop across cake and medium
r = Specific cake resistance
µ = Filtrate viscosity
l = Cake thickness and
L = Thickness of cake equivalent to medium resistance

Kozeny-Carman equation has certain limitations that it does not take into account the depth of the granular bed which is lesser than the actual path travelled by the fluid. The actual path is not straight throughout the bed, but it is sinuous or tortuous.

Poiseulle’s Law:

This law considers that filtration is similar to the streamline flow of a liquid under pressure through capillaries. It can be expressed as;

\frac1{dv}\frac A{dt}=\frac{\triangle P}{µ\;(Rm\;+\;Rc)}

Cake\;resis\tan ce\;(Rm)\;=\frac{\sigma W}A

Specific cake resistance (σ) = σ’∆P^s

The filter resistance is much less than the cake resistance i.e. Rc << Rm. Therefore, on rearranging equation first equation:

\frac1{dv}\frac A{dt}=\frac1{\sigma\;(\sigma'\;\triangle P^s\;\times\;WA)}

Where, V = Filtrate volume (L)
A = Filter area ( m² )
t = Time (h)
∆P = Pressure driving force (N)
µ = Broth viscosity (Pa.s) m²/h
W = Mass of filter (kg)
R = Resistance (m^-1)
σ = Specific cake resistance (m/kg)
S = Compressibility factor

Darcy’s Equation:

When using the Poiseulle equation for filtration, it is considered that capillaries in the filter medium are highly irregular and non-uniform. In order to approximate the flow rate, the height of the cake is taken as the length of the capillaries, and correction factors are introduced for the radius of the capillaries. This makes the flow rate simpler and is expressed as

U\;=\;\frac{KA\;\triangle P}{\eta L}

Where, U = Flow rate (L/sec)
K = Permeability coefficient of the cake (m²)
A = Surface area of filter medium (m²)
∆P = Pressure difference across the filter, Pa
r = Capillary radius in filter bed (m)
L = Capillary length (m)
Η = Viscosity of liquid (Pa.s)

The permeability coefficient (K) in the last eq. depends on the porosity, specific surface area, and compressibility of the cake. This coefficient may be defined as the flow rate of a liquid of unit viscosity across a unit area of cake with a unit thickness under a unit pressure gradient.

Factors influencing filtration