Table of Contents
Water Is an Nucleophile
Lone pairs of electrons from electron-rich compounds called nucleophiles attack electron-poor atoms called electrophiles frequently in metabolic reactions. Electrophiles and nucleophiles don’t always have a formal negative or positive charge. Water is an efficient nucleophile because its two lone pairs of sp3 electrons have a partial negative charge. The oxygen atoms of phosphates, alcohols, and carboxylic acids; the sulfur of thiols; and the nitrogen atoms of amines and the imidazole ring of histidine are all important nucleophiles in biology. Common electrophiles include the carbonyl carbons in amides, esters, aldehydes, and ketones and the phosphorus atoms of phosphoesters.
The amide, glycoside, or ester linkages that hold biopolymers together are often cleaved by nucleophilic attack by water. Hydrolysis is the name for this process. Water is a product when monomer units are brought together to produce biopolymers like proteins or glycogen, such as during the formation of a peptide bond between two amino acids, for example.
While hydrolysis is a thermodynamically favorable reaction, polypeptide and oligonucleotide amide and phosphoester linkages are stable in the cell’s aqueous environment. The thermodynamics that regulates a reaction’s equilibrium point does not determine the rate at which it will proceed toward its equilibrium point, resulting in this seemingly counterintuitive phenomenon. When needed, enzymes, which are protein catalysts, speed up the rate of hydrolytic reactions in the cell. Nucleases catalyze the hydrolysis of phosphoester linkages in DNA and RNA, while proteases catalyze the breakdown of proteins into their component amino acids. Careful control of the activities of these enzymes is required to ensure that they act only at appropriate times.
Many Metabolic Reactions Involve Group Transfer
The transfer of a chemical group G from a donor D to an acceptor A to produce an acceptor group complex, A—G:, is involved in many of the enzymic processes responsible for the synthesis and breakdown of biomolecules.
D´G+A=A´G+D
The transfer of glucosyl groups to water or orthophosphate occurs during the hydrolysis and phosphorolysis of glycogen, for example.
The generation of split products is significantly favored by the equilibrium constant for the hydrolysis of covalent bonds.
In contrast, many group transfer processes involved in macromolecule biosynthesis entail the production of thermodynamically unfavorable covalent bonds. Under their ability to directly link two ordinarily independent reactions, enzyme catalysts play a vital role in overcoming these barriers.
A novel coupled process can be formed by coupling an energetically unfavorable group transfer reaction with a thermodynamically advantageous reaction, such as ATP hydrolysis, whose net overall change in free energy promotes biopolymer synthesis.
Why are biopolymers like proteins and DNA relatively durable, given the nucleophilic nature of water and its high concentration in cells? And how may biopolymer synthesis take place in an aqueous environment that favors hydrolysis?
The properties of enzymes lie at the heart of both problems. Even highly favored thermodynamically processes do not necessarily occur quickly in the absence of enzymic catalysis.
The physiologic conditions under which a given biopolymer will be generated or destroyed are determined by precise and differential control of enzyme activity and the sequestration of enzymes in certain organelles. Biopolymer synthesis is made easier by enzyme active sites’ capacity to sequester substrates in an environment free of water.
Water Molecules Exhibit a Slight but Important Tendency to Dissociate
While the ability of water to ionize is minor, it is critical for life. Water’s ionization can be depicted as an intermolecular proton transfer that produces a hydronium ion (H3O+) and a hydroxide ion (OH), because it can behave as both an acid and a base:
H2O+H2O=H3O+OH−
A cluster of water molecules is truly linked with the transferred proton. In solution, protons exist not only as H3O+ but also as multimers as H5O2+ and H7O3+. Even though the proton is extremely hydrated, it is commonly represented as H+.
Individual hydrogen or oxygen atoms cannot be said to be present as an ion or as part of a water molecule since hydronium and hydroxide ions constantly recombine to produce water molecules. It’s an ionone moment, and then it’s a part of a water molecule the next. As a result, individual ions or molecules are not taken into account. Instead, we’re talking about the likelihood that specific hydrogen will be present as an ion or as part of a water molecule at any given time. The ionization of water may be statistically described since 1 g of water has 3.46 1022 molecules.
The probability that a hydrogen atom exists as an ion is 0.01; this indicates that a hydrogen atom has 1 in 100 possibilities of being an ion and 99 out of 100 chances of being part of a water molecule at any given time. The probability of a hydrogen atom becoming a hydrogen ion in pure water is roughly 1.8 109. As a result, the chances of it being a part of a water molecule are nearly equal. To put it another way, there are 0.56 billion or 0.56 109 water molecules in pure water for every hydrogen or hydroxide ion. Despite this, hydrogen and hydroxide ions play an important role in the characteristics of water.
When it comes to water dissociation,
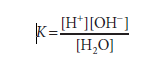
where molar concentrations (strictly speaking, molar activities) are represented by brackets and K is the dissociation constant.
1 liter (L) (1000 g) of water contains 1000/18 = 55.56 mol because 1 mole (mol) of water weighs 18 g. The molar mass of pure water is thus 55.56. The molar concentration of H+ ions (or of OH ions) in pure water is the product of the likelihood, 1.8×10-9, times the molar concentration of water, 55.56 mol/L, since the probability that hydrogen in pure water will exist as a hydrogen ion is 1.8×10-9. 1.0×10-7 mol/L is the result.
For pure water, we can now compute the dissociation constant K:
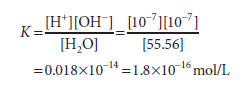
The molar concentration of water, 55.56 mol/L, is too great to be significantly affected by dissociation. It is therefore considered to be essentially constant. This constant may therefore be incorporated into the dissociation constant K to provide a useful new constant Kw termed the ion product for water. The relationship between Kw and K is shown below:
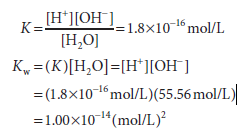
Note that the dimensions of K are moles per liter and those of Kw are moles2 per liter2 As its name suggests, the ion product Kw is numerically equal to the product of the molar concentrations of H+ and OH–:
Kw =[H+][OH–]
At 25°C, Kw = (10-7)2, or 10-14(mol/L)2. At temperatures below 25°C, Kw is somewhat less than 10-14, and at temperatures above 25°C it is somewhat greater than 10-14. Within the stated limitations of temperature, Kw equals 10-14 (mol/L)2 for all aqueous solutions, even solutions of acids or bases. We use Kw to calculate the pH of acidic and basic solutions.
Make sure check our other amazing article Water and pH